Racine douzième de deux
Ne vous enfuyez pas tout de suite en voyant ce titre ! Promis, on ne va pas parler que de maths… enfin, pour être précis, les maths ne sont pas le sujet principal de cet article.
Racine douxième de deux
💡 En lisant ce titre, vous avez sans doute eu une de ces deux réactions :
Si vous appartenez à la première catégorie, vous vous demandez sûrement quel rapport il existe entre la racine douxième de deux (à peu près 1,059463094), et la musique.
Commençons par le commencement et donnons le LA.
Le « 440 Hz » est une convention (pas toujours suivie d'ailleurs), mais peu importe.
💡 On s'est vite rendu compte qu'on pouvait multiplier ou diviser par deux la fréquence d'une note et obtenir des notes à la consonance quasi-parfaite : des vibrations à 220 Hz, 440 Hz ou 880 Hz donnent trois notes, une grave, une médium et une plus aiguë… mais qui à part ça semblent parfaitement similaires.
(Oui, c'est pas facile à expliquer.)
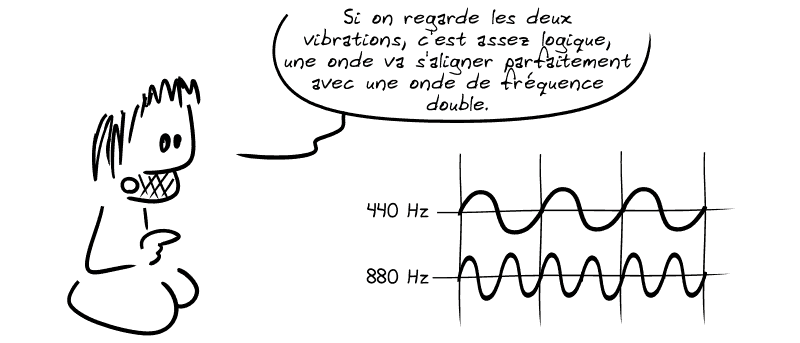
De là, deux choses :
▶️ D'abord, on a donné le même nom à ces notes.
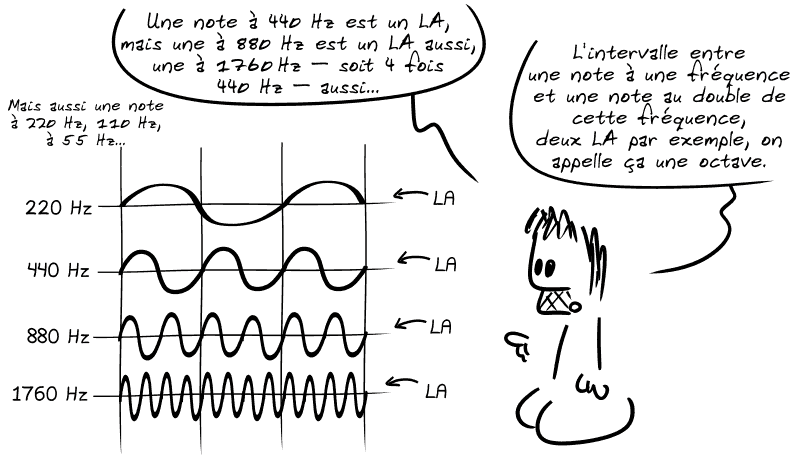
▶️ Ensuite, on en a déduit que l'oreille humaine avait une sensibilité logarithmique aux vibrations sonores :
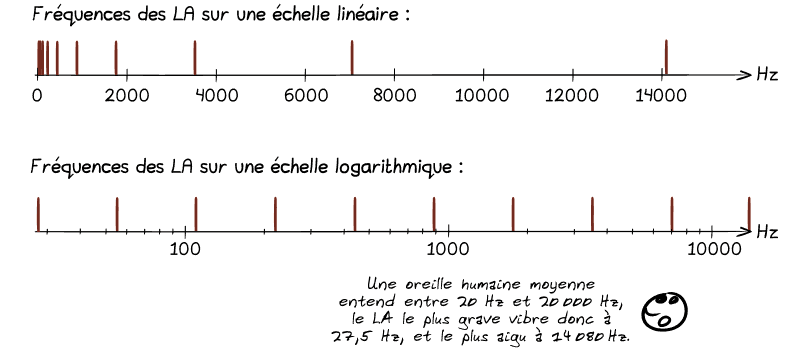
Bon, on a pondu un paquet de LA, d'accord, mais qu'en est-il des autres notes ?
💡 Eh bien admettons par exemple qu'on prenne la fréquence moyenne entre les deux LA précédents, soit la fréquence du LA à 440 Hz multiplié par 1,5 (soit 3/2).
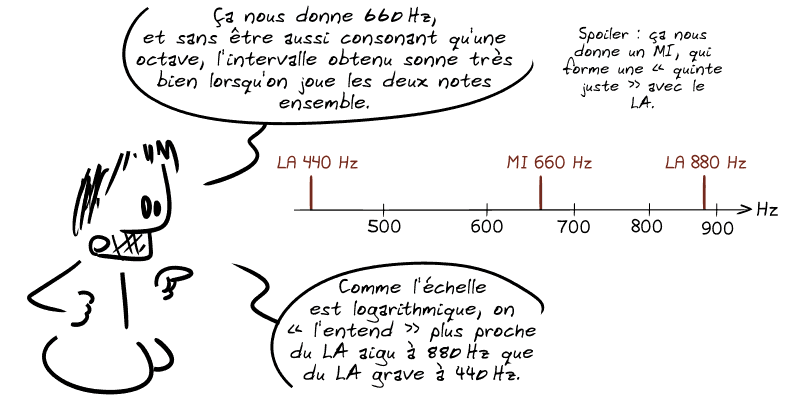
On peut répéter ce processus en partant cette fois du nouveau MI obtenu.
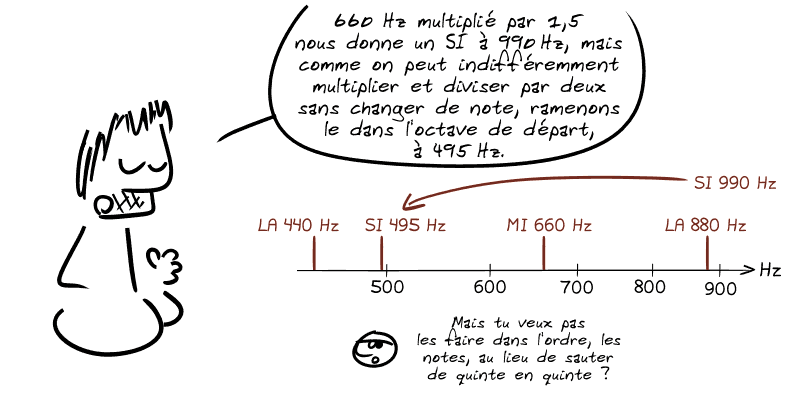
Au bout de 12 fois, on retombe sur notre LA de départ…
⚠️ Ou presque !
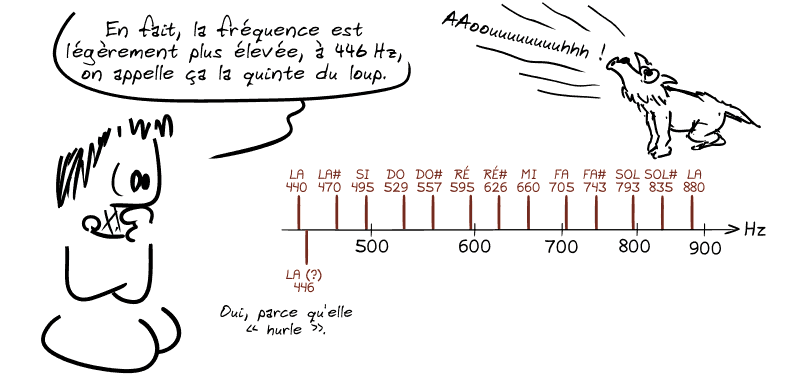
▶️ On peut remarquer que les douze notes produites sont quasiment distribuées régulièrement sur notre échelle logarithmique…
⚠️ Pour espacer douze valeurs régulièrement, on prendrait normalement la différence entre le maximum et le minimum et on diviserait par douze… mais rappelez-vous qu'on est en échelle logarithmique !
Il ne faut pas que ce soit la différence entre deux valeurs qui soit constante mais le rapport : on doit donc trouver le nombre qui, multiplié 12 fois par lui-même, donne 2…
Ce nombre, c'est racine douzième de deux.
▶️ En multipliant la fréquence d'une note par racine douzième de deux, on tombe quasiment sur la note obtenue par l'enchaînement des quintes… tout en s'assurant de bien retomber sur la même note à l'octave suivante à la fin, sans quinte du loup, et en retrouvant les mêmes fréquences quelle que soit la note de départ !
💡 Et avant, on utilisait quoi ? Eh bien, par exemple, la gamme pythagoricienne, celle construite avec la succession de quintes…
⚠️ La gamme tempérée qui utilise racine douzième de deux nous simplifie donc grandement la vie, même si les fréquences des différentes notes ne s'accordent en réalité pas exactement entre elles…
💡 Pour finir, vous allez peut-être me demander… mais pourquoi a-t-on donc donné un nom simple à 7 d'entre ces 12 notes (do, ré, mi, fa, sol, la, si) et pourquoi les 5 autres sont-elles nommées avec des dièses (ou des bémols) ?
Bref, en théorie musicale, la limite entre physique acoustique et conventions, c'est un sujet qui n'est pas
🛈 Si vous avez aimé cet article, vous pouvez le retrouver dans le livre Grise Bouille, Tome VI.
