Un demi de compression

Un demi de compression

✷ Voir l'article Des zéros et des uns.

Reprenons.

💡 Avec des zéros et des uns, on peut donc enregistrer n'importe quelle information (texte, son, image, etc.). Seulement, on veut stocker beaucoup de choses et les octets sont en nombre limités.

▶️ Du coup, stocker chaque information de manière « brute » est rarement une solution acceptable : on va chercher à réduire la place nécessaire pour stocker une information. Ça s'appelle la compression.

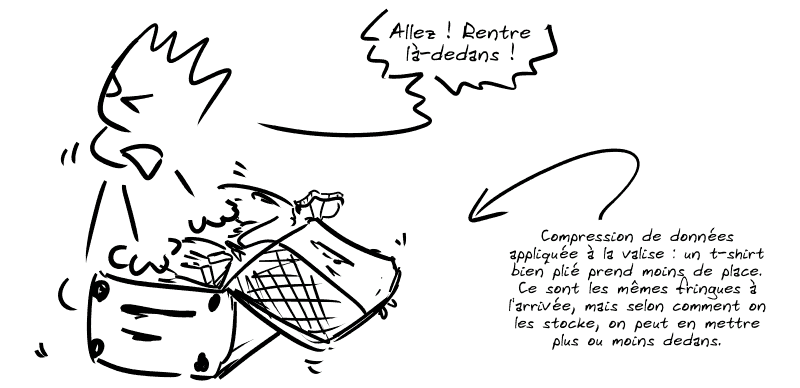
Par exemple, pour stocker des textes, on peut simplement associer à chaque caractère (chaque lettre, chiffre ou signe de ponctuation) une suite de bits de taille fixe.

C'est l'idée derrière la table ASCII :

En code ASCII, chaque caractère prend 1 octet (soit 8 bits*) :

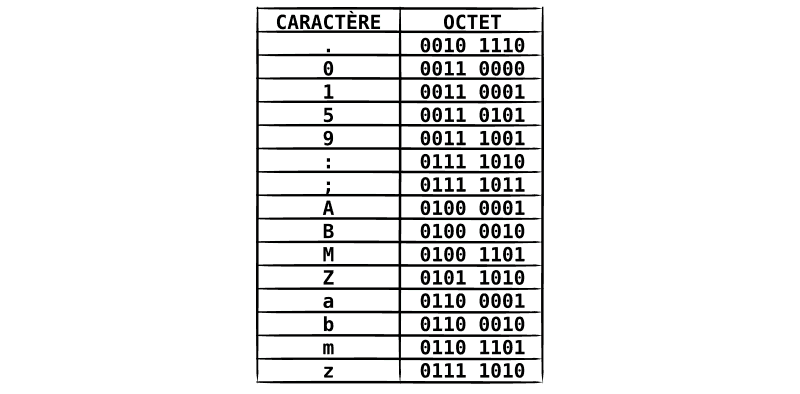
✷ 7 bits à la base, mais on l'a étendue à 8 bits par la suite.

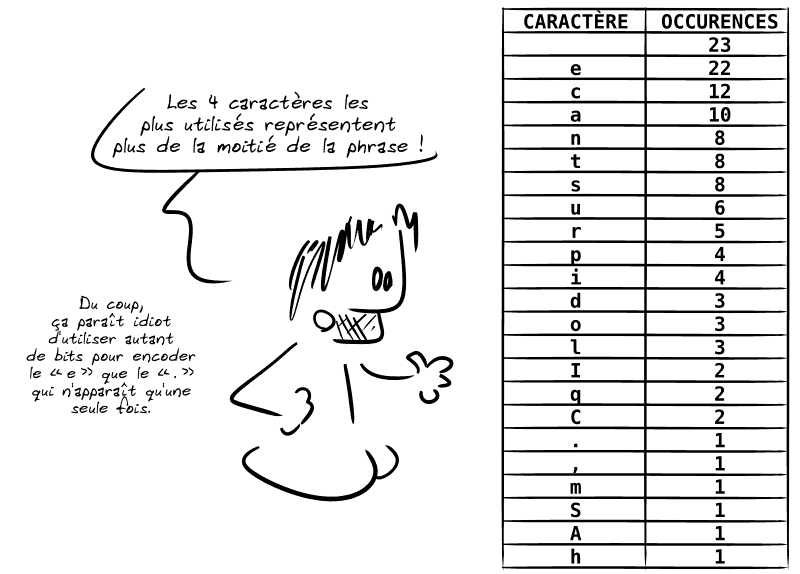
💡 Tout d'abord, remarquons que 8 bits permettent de représenter 256 valeurs (2⁸) et donc de différencier 256 caractères… oui, mais notre phrase utilise beaucoup moins de caractères !

131 caractères de 5 bits nous donneraient donc 655 bits, soit 82 octets (un gain de 38 % par rapport à la taille en ASCII sur 8 bits).

▶️ On peut aussi remarquer que les caractères ne sont pas tous autant utilisés les uns que les autres :

💡 Imaginons alors que nous utilisions l'arbre suivant à la fois pour encoder et décoder des caractères.

On part de la racine : à chaque fois que l'on tourne à gauche, on met un 0 ; à chaque fois qu'on tourne à droite, on met un 1.

Quand on atteint une feuille, on atteint un caractère et on a donc le code correspondant au caractère.

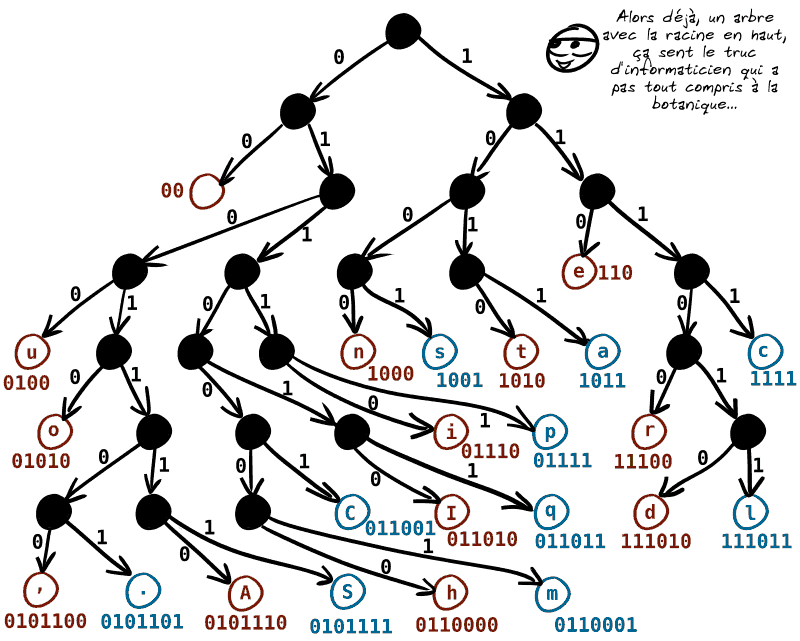
Pour le décodage, c'est simple : quand on lit le fichier, on part de la racine et les 0 et les 1 indiquent quelle direction prendre. Quand on atteint une feuille, on a lu un caractère, et on repart d'en haut.

▶️ Chaque caractère peut donc avoir un code binaire de taille différente (plus il est haut dans l'arbre, plus le code est court).

Et comme on a mis les caractères qui apparaissent souvent plutôt vers le haut de l'arbre…

PAF !

Au total, notre texte n'occupe plus que 514 bits (au lieu des 655 en utilisant un codage régulier sur 5 bits, soit un gain de 22 %).

▶️ Eh bien figurez-vous qu'on peut facilement généraliser cela à tous les textes français : en effet, on sait statistiquement que le « e » apparaît beaucoup plus que le « z » ou le « w » dans notre langue.

Bien sûr, pour le Scrabble comme pour la compression, les fréquences (et donc les valeurs) varient selon la langue.

⚠️ En réalité, pour la compression, en général, on ne présuppose pas d'une langue ou d'une autre : on construit dynamiquement l'arbre le plus adapté à ce que l'on veut compresser.

💡 L'arbre que j'ai utilisé ci-dessus ne sort pas de nulle part, il vient du principe du codage de Huffman mis au point en 1952 par David A. Huffman pendant sa thèse au MIT.

On parle d'un codage encore utilisé aujourd'hui dans pratiquement tout ce qui est numérique : Huffman fait partie de ces personnes qui ont bien plus révolutionné l'informatique que des Steve Jobs ou des Bill Gates, mais qu'on connaît beaucoup moins.

Après c'est sûr, un universitaire passionné par les mathématiques des origamis, face à un milliardaire qui fait poser des filets anti-suicide dans ses usines en Chine, ça fait pas le poids.

Alors rendons hommage à ce grand monsieur (hommage posthume, car il nous a quittés en 1999).

💡 Notez que la plupart des formats de compression que vous connaissez (les ZIP, GZIP, etc.) utilisent un codage légèrement différent de celui de Huffman (codage par dictionnaire), mais qui repose sur le même principe universel dans la compression de données : identifier les informations redondantes et les encoder beaucoup plus succinctement que les informations rares.

Ainsi, on peut stocker la même information (aucune perte) en prenant moins de place en moyenne !