Blog BD satirique

Le lien a été copié dans le presse-papier.

Parallèles (mais presque)

Publié le 26 mars 2021 par Gee

Un peu de géométrie aujourd’hui ! Ça peut valoir le coup de (re)lire mon article sur l’infini avant, vu qu’on va pas mal parler d’infini aussi ici…

Parallèles (mais presque)

💡 Cet énième titre désopilant de poilitude jeu-de-motesque vous annonce le sujet du jour : la géométrie, et notamment le parallélisme.

Le smiley, l'air complétement blasé : « Trop bien. On va s'marrer. J'ai déjà mal au ventre. Pitié pour mes zygomatiques. Hahaha. » Gee, énervé : « Dis, tu vas pas commencer, toi. »

Comme vous le savez sans doute, on dit que deux droites sont parallèles si elles ne se coupent pas.

Gee, représenté entre deux droites, une sur sa tête dans la direction de son regard, une sous ses pieds dans la direction opposée (les deux ne se croisent pas). Il précise donc : « En 2D uniquement, hein. En 3D, deux droites qui ne se coupent pas ne sont pas forcément parallèles, elles sont peut-être simplement dans deux plans différents. » Le smiley, souriant : « La définition qui marche dans n'importe quelle dimension, c'est que deux droites parallèles ont des vecteurs directeurs colinéaires, mais Gee voulait éviter de faire fuir son public dès la deuxième image, comme d'hab… »

⚠️ Vous avez peut-être déjà entendu une personne voulant faire son intéressante vous dire :

Un mec lambda qui fait le malin en souriant : « Mais en fait, deux droites parallèles se coupent à l'infini ! Ah ! T'es bien feinté, là, hein ? » Gee, un peu blasé : « Mmh… »

Alors… est-ce que deux droites parallèles se coupent à l'infini ?

En fait, c'est une façon assez maladroite de présenter les choses…

Gee se positionne sur un repère 2D : « Mettons que je place un point P sur l'axe des abscisses et que je trace une droite D entre ce point et un point de coordonnées (0,1). Le point P est le point d'intersection entre la droite D et l'axe des abscisses Dx. Appelons a l'angle formé entre la droite D et l'axe des ordonnées Dy. » Le smiley, tout sourire : « Je suis le smiley S. Bonjour, internaute I. »

💡 C'est le moment d'appeler notre ami Sohcahtoa !

Gee précise : « Sohcahtoa est un Pokémon de type mnémotechnique vous permettant de vous souvenir quoi diviser par quoi pour calculer un sinus, un cosinus ou une tangente. » Une créature étrange, avec une corne de licorne et une queue de renard, agite les bras en braillant : « Sohcahtoaaa ! Soh ! Caah ! Tooaaaaa ! Sinus = Opposé sur Hypoténuse, Cosinus = Adjacent sur Hypoténuse, Tangente = Opposé sur Adjacent. »

Gee, qui s'amuse beaucoup : « L'hypoténuse étant un Pokémon de type cheval galopant en général du côté le plus long du triangle rectangle – en face de l'angle droit. » Une tête de cheval posée sur le côté long d'un triangle rectangle, l'air désespéré : « Tuez-moi. »

Dans notre cas, si on regarde l'angle a entre l'axe des ordonnées Dy et la droite D, la coordonnée xP correspond au côté opposé. Le côté adjacent est connu, il mesure 1.

Un prof à collier de barbe taquine : « Un quoi ? Un mètre ? Un centimètre ? Un pamplemousse ? » Gee le fait partir avec impatience : « Ah non non non, j'ai pas le temps pour les profs de maths obsédés par les fruits, c'est “un” de l'unité que vous voulez, disons : 1 OSEF. »

▶️ On peut donc facilement exprimer l'angle a en fonction de la position du point P sur l'axe des X (qui correspond à la taille du côté opposé).

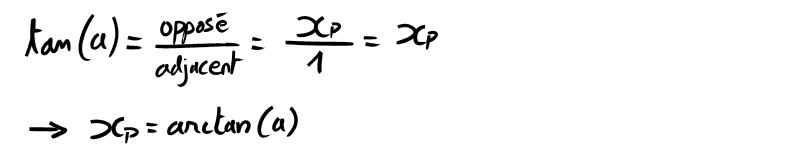
Une formule : la tangente de a est égale à opposée sur adjacent, donc à xp sur 1, donc à xp. Donc xp est égale à l'arc tangente de a.

Gee, toujours placé sur son repère 2D (où on a ajouté le côté adjacent et opposé) : « L'arc tangente étant la fonction réciproque à la fonction tangente. » La Geekette fait mine de partir : « Ouais, bah moi, je vais prendre l'arc tangente… » Gee : « Donc tu vas rester là ? » La Geekette : « Euuuh… »

Comment évolue cet angle quand le point P s'éloigne de l'origine ?

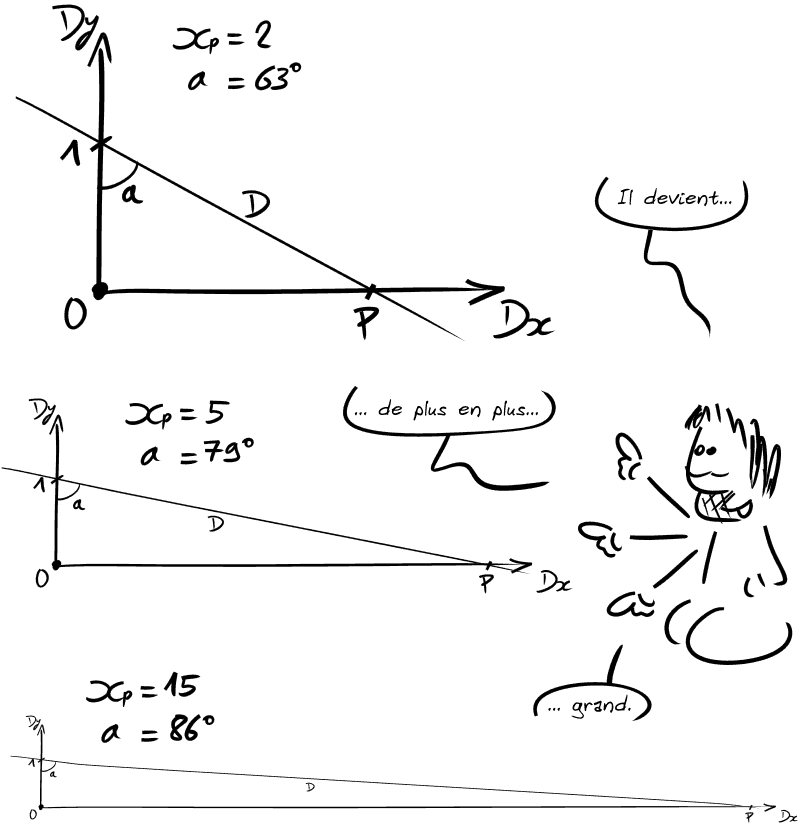
Gee à côté de trois repères où le point P est de plus en plus loin de l'origine et où l'angle se rapproche de plus en plus d'un angle droit : « Il devient de plus en plus grand. »

▶️ On peut le calculer, mais on peut aussi simplement en avoir l'intuition en regardant les images ci-dessus : plus P s'éloigne, plus l'angle se rapproche de 90°.

La Geekette : « Ça fait chaud. » Gee, les bras croisés : « Tout dépend. En Kelvin, ça caille plutôt sévère. » La Geekette : « Pas faux. » Gee : « Mais vu qu'on parle de degrés angulaires, je vois pas bien le rapport. » La Geekette : « J'aime bien perturber tes BD. »

Quand la distance entre P et l'origine tend vers +∞, l'angle tend vers 90°.

Les droites deviennent donc de plus en plus proches d'être parallèles

(puisque D devient proche d'être perpendiculaire à l'axe des ordonnées, auquel l'axe des abscisses est lui aussi perpendiculaire, vous suivez ?).

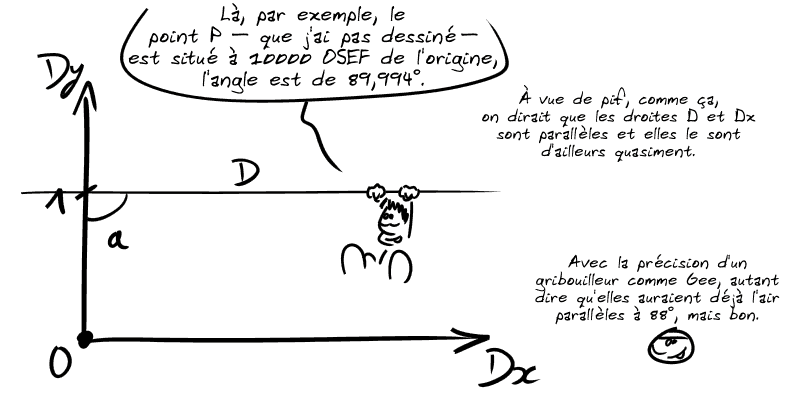
Gee, accroché à la droite D qui est quasiment horizontale : « Là, par exemple, le point P – que j'ai pas dessiné – est situé à 10000 OSEF de l'origine, l'angle est de 89,994°. À vue de pif, comme ça, on dirait que les droites D et Dx sont parallèles et elles le sont d'ailleurs quasiment. » Le smiley, goguenard : « Avec la précision d'un gribouilleur comme Gee, autant dire qu'elles auraient déjà l'air parallèles à 88°, mais bon. »

💡 On pourrait donc hâtivement dire que si P est vraiment situé infiniment loin de l'origine, l'angle formé devient exactement 90°, les droites sont donc parallèles, avec un point d'intersection P à l'infini.

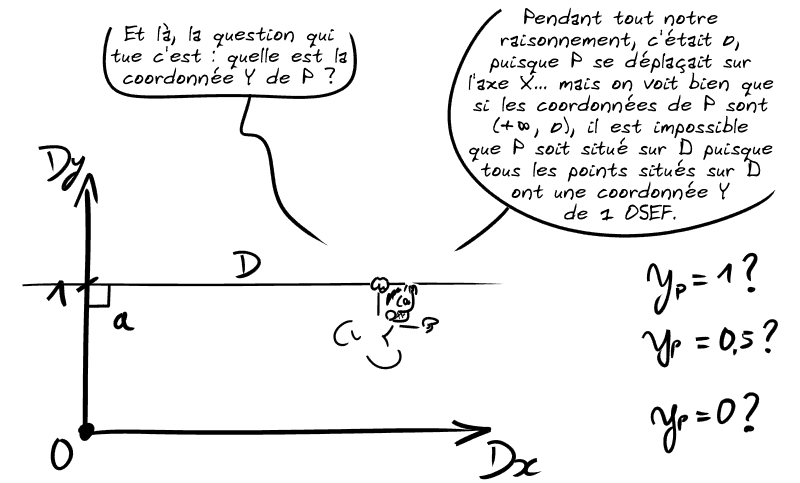
Gee, toujours accroché à D qui est maintenant complétement horizontale, avec a qui est un angle droit : « Et là, la question qui tue c'est : quelle est la coordonnée Y de P ? Pendant tout notre raisonnement, c'était 0, puisque P se déplaçait sur l'axe X… mais on voit bien que si les coordonnées de P sont (+∞, 0), il est impossible que P soit situé sur D puisque tous les points situés sur D ont une coordonnée Y de 1 OSEF. » Alors, yp est égale à 1 ? À 0,5 ? À 0 ?

⚠️ J'en avais déjà causé dans mon article sur l'infini : en géométrie Euclidienne, l'infini est une limite et ne fait pas partie de l'espace, un point ne peut donc pas être « à l'infini », ça n'a pas de sens.

Gee explique : « Deux droites parallèles ne se coupent JAMAIS dans un espace Euclidien, point. Lorsque deux droites tendent à devenir parallèles, leur point d'intersection tend à se déplacer infiniment loin. Mais c'est une limite. » Le smiley commente : « C'est comme moi. Au fur et à mesure de cette BD, je tends à comprendre, mais c'est une limite. En vrai, j'ai rien pigé. »

▶️ Pour finir, notons qu'il existe d'autres cas où on peut définir un point d'intersection pour deux droites parallèles : la géométrie projective, par exemple, le permet.

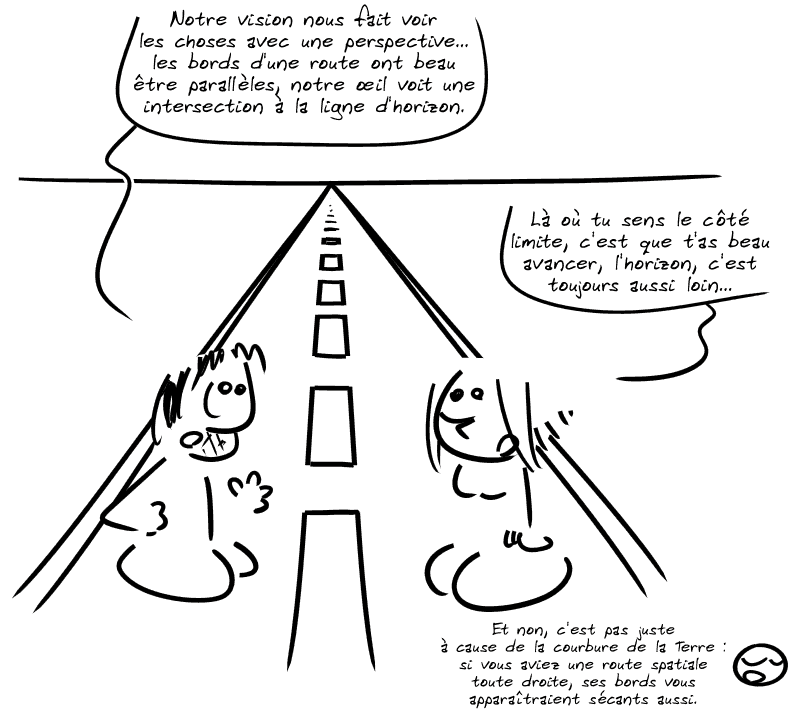
On voit une route toute droite et la ligne d'horizon où toutes les lignes se rejoignent. Gee, sur la route, explique : « Notre vision nous fait voir les choses avec une perspective… les bords d'une route ont beau être parallèles, notre œil voit une intersection à la ligne d'horizon. » La Geekette, à côté : « Là où tu sens le côté limite, c'est que t'as beau avancer, l'horizon, c'est toujours aussi loin… » Le smiley précise : « Et non, c'est pas juste à cause de la courbure de la Terre : si vous aviez une route spatiale toute droite, ses bords vous apparaîtraient sécants aussi. »

Et sur cette considération aussi géométrique que philosophique sur l'horizon, je vous dis au revoir de façon péremptoire.

Le smiley tire la langue en rigolant : « Ça c'était pour les gens qui ont attendu la réf à Kaamelott pendant tout l'article. » Note : BD sous licence CC BY SA (grisebouille.net), dessinée le 25 mars 2021 par Gee.

Publié le 26 mars 2021 par Gee
Tu sais quoi ?

Des bandes-dessinées visant à traiter de sujets variés – science, langage, histoire, anecdotes – avec humour tout en essayant d’apporter, pourquoi pas, une valeur ajoutée instructive : vulgarisation scientifique, analyse culturelle ou sociale…

Cet article est inclus dans

Couverture du livre

Grise Bouille, Tome V — Recueil de bandes dessinées mêlant humour, vulgarisation scientifique et satire politique.

Dessins 100 % humains, garantis sans IA, réalisés avec amour

Ce blog n'utilise aucune IA générative ; les scénarios ne sont pas écrits par un programme informatique ; les dessins sont entièrement faits main à la tablette graphique par un auteur-dessinateur humain.

Soutenir

Ce blog est publié sous licence libre, il est librement copiable, partageable, modifiable et réutilisable. Il est gratuit car soutenu par un financement participatif permanent. Sans inscription, vous pouvez très simplement participer à débloquer des paliers supplémentaires :

Pour le mois prochain (octobre 2025), 307 € ont été récoltés, débloquant 2 paliers sur 12 :

Pour la saison en cours (2025-2026), 307 € ont été récoltés, débloquant 0 méta-palier sur 3 :

Note : pour plus d'informations sur les paliers et méta-paliers, voir la page crowdfunding.