Vers l’infini
J’en avais déjà parlé brièvement à l’époque du Geektionnerd (et oui, j’ai recyclé quelques blagues, QUOI KESKYA), voici un petit article sur l’infini et ce qu’il représente dans différents domaines…
Vers l'infini
L'infini est quelque chose qui est caractérisé par le fait de n'avoir pas de limite en taille.
Commençons par un peu de typographie :
le symbole désignant l'infini est ∞ et il a été inventé par John Wallis, un mathématicien
principalement connu pour avoir inventé le symbole désignant l'infini.
Cette anecdote n'est qu'une théorie, en fait on ne sait pas trop pourquoi il y a choisi ce symbole. Par contre, ça a l'air idiot, mais en fait il y a beaucoup de cas où « infini » veut dire « beaucoup ». On va y revenir…
En mathématiques, l'infini est un concept relativement simple : c'est un nombre plus grand que tous les autres (ou plus petit s'il est négatif).
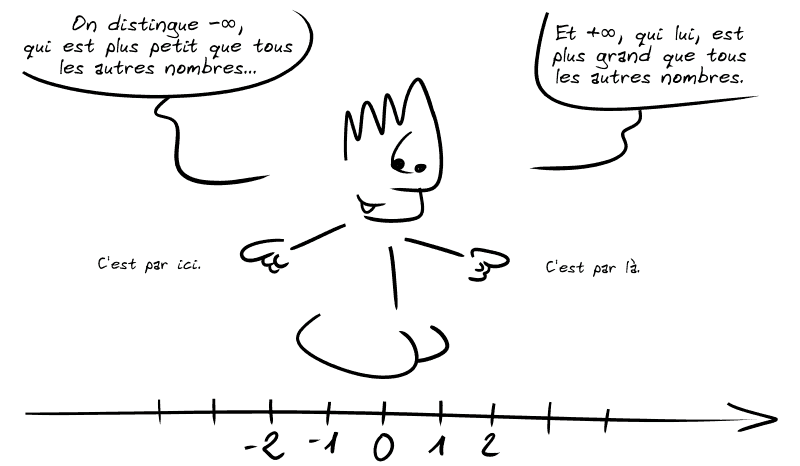
Oui, c'est « par ici » ou « par là », parce que bien sûr, on ne peut pas placer l'infini sur un axe représentant les nombres de façon linéaire (sinon, on pourrait mettre un autre nombre plus grand derrière, et un tel nombre n'est pas censé exister).
Techniquement, l'infini n'est d'ailleurs pas un nombre « comme les autres », et il n'appartient de toute façon pas à l'ensemble des nombres réels ℝ.
Si les infinis ne sont pas des réels, on peut néanmoins généraliser quelques opérations comme l'addition et la multiplication.
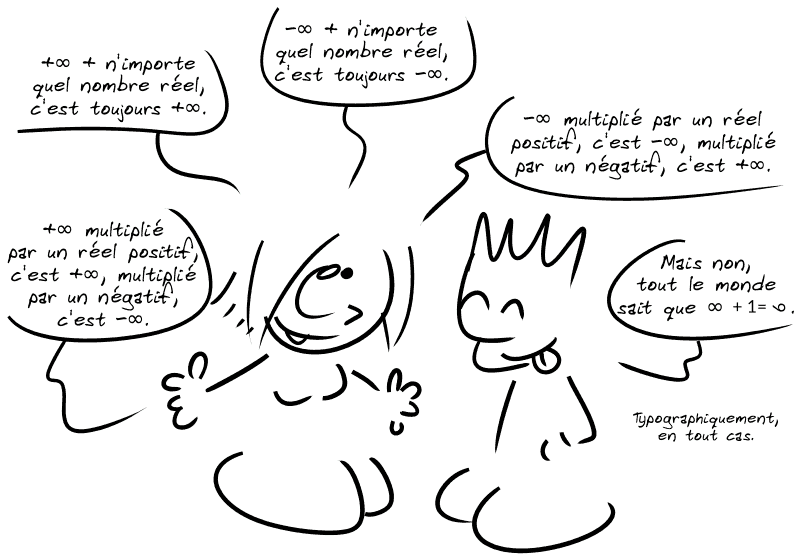
Après, les opérations entre infinis, les divisions, les multiplications entre infini et 0, tout ça, c'est tout de suite plus compliqué.
On pourrait hâtivement dire que l'infini est l'inverse de zéro, sauf que…
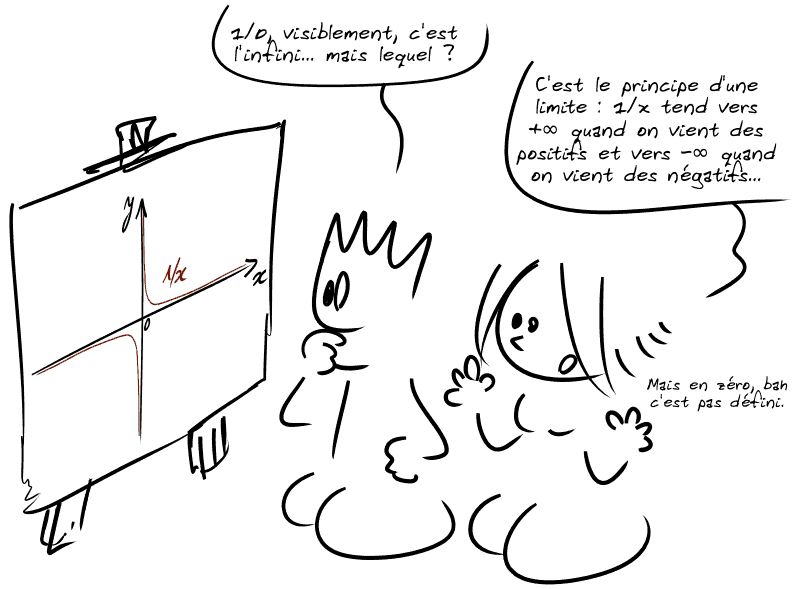
En sciences physiques, par contre, on s'embête beaucoup moins avec ces notions compliquées : l'infini, c'est un truc grand.
En fait, tout est question de proportions : si un objet, une distance, etc., est très largement plus grand que les autres dans une situation donnée, considérer cette chose comme infinie ne produit que des erreurs négligeables de calcul tout en simplifiant grandement les modélisations.
Dans l'exemple du dessus, on peut considérer que 3 m = +∞ car l'objet ciblé – un fil à plomb – est minuscule.
J'en parlais dans mon article En fait, Einstein se trompait :
Considérer que la Terre est plate localement, ça revient à dire que son centre est à l'infini (la sphère tend localement vers un plan quand le centre s'éloigne à l'infini).
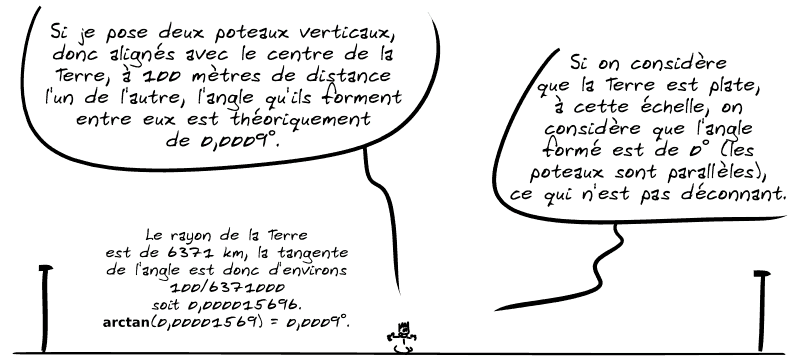
Bref, les sciences physiques sont des sciences de gorets qui ont le même niveau de rigueur que les livreurs qui t'annoncent une fourchette d'horaire de livraison ont une vision de l'infini relative à une taille donnée qui correspond d'ailleurs beaucoup à celle de tous les jours.
Le lectorat avisé aura compris que l'infini spatial est communément appelé Perpète-lès-Oies (ou Pétaouchnock) tandis que l'infini temporel – aussi dénommé éternité – est désigné par Saint-Glinglin (ou les Calendes Grecques, etc.).
Ceci étant dit, pour de nombreux domaines, la question reste entière : est-ce que l'infini existe dans notre monde physique ?
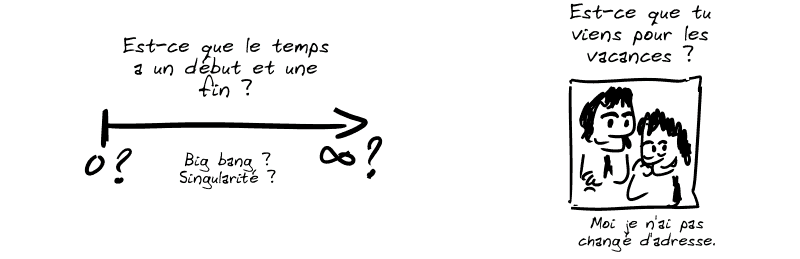
Le truc, c'est qu'on risque fort de ne jamais pouvoir formellement répondre à cette question : en effet, pour prouver qu'un infini (distance, temps ou autre) existe dans l'univers, il faudrait pouvoir le mesurer… ce qui semble compromis puisque nous (et nos outils) ne sommes pas infinis ni éternels, justement.
Bref, on atteint les limites de nos connaissances et on flirte presque avec la métaphysique dans certains cas.
Parlons enfin de l'infini en informatique (oui, vous ne pensiez quand même pas que vous alliez y échapper ?).
En termes d'angoisse existentielle, on est déjà plus pépouzes.
Bon, faut admettre que c'est encore plus simple qu'en sciences physiques, puisqu'un ordinateur étant fini, il ne peut représenter qu'un nombre fini de nombres.
Je ne sais pas si je suis très clair.
De là à dire que les ordinateurs, c'est rien que des feignasses, bon.
Concluons sur une toute dernière chose qui n'est pas infinie :
🛈 Si vous avez aimé cet article, vous pouvez le retrouver dans le livre Grise Bouille, Tome IV.
