La quatrième dimension

La quatrième dimension

💡 Au commencement était la première dimension, X. À ce moment-là, les choses étaient simples, on avançait en ligne droite, pépouze. Le monde était peuplé de points, de segments, de demi-droites et de droites qui se marchaient quand même pas mal sur les pieds…

💡 Ensuite, on inventa la seconde dimension, Y, perpendiculaire à la première. Ainsi naquirent les mondes 2D (comme le Royaume Champignon), ce qui permit aux surfaces de s'épanouir.

💡 Puis vint Z, la troisième dimension, perpendiculaire aux deux autres, et l'avènement des volumes (et de notre univers physique propre, soit dit en passant).

Et lorsque l'on pose la question « qu'est-ce que la quatrième dimension ? », un chœur uniforme et sûr de lui s'exclame :

Passons sur la fameuse série de SF (The Twilight Zone) qui faisait d'ailleurs allusion en VO à la cinquième dimension, pas la quatrième – mais c'est la conversion dollar/franc qui a foutu le bazar là-dedans (enfin, je crois).

⚠ Alors il va falloir arrêter de penser automatiquement au temps dès qu'on vous cause de dimension supérieure à 3.

Déjà parce qu'à partir de là, si je vous demande quelle est la cinquième dimension, vous allez galérer.

Ensuite, parce qu'il ne vous aura pas échappé que les espaces 1D, 2D et 3D dont je parlais ont des dimensions de même type (spatiales) qui permettent notamment de faire des calculs géométriques avec.

⚠ Si vous essayez d'étendre ce genre de formule avec une dimension qui n'est pas spatiale (genre le temps), vous allez avoir un petit problème d'homogénéité dans votre formule.

En termes simples :

Je sais ce que vous allez me dire : oui, mais si on multiplie la quatrième dimension par la vitesse (au hasard, celle de la lumière), PAF ! C'est homogène, merci, au revoir messieurs-dames.

💡 C'est l'idée derrière la notion « d'espace-temps », utilisée dans les théories de la relativité, qui n'est plus un espace Euclidien mais pseudo-Euclidien (espace de Minkowski pour être précis).

Mais laissons Minkowski tranquille et restons avec ce bon vieil Euclide.

On peut tout à fait définir des dimensions spatiales supérieures, sur le même principe que X, Y et Z.

Tous les calculs possibles en 1D, 2D, 3D se généralisent en 4D, 5D, 6D, etc. Et les objets géométriques aussi :

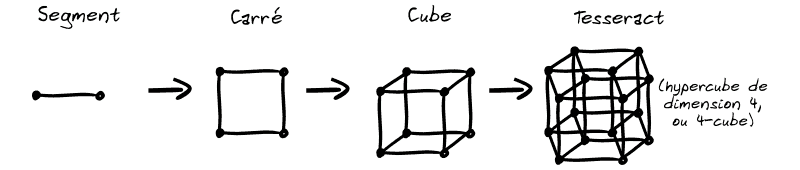
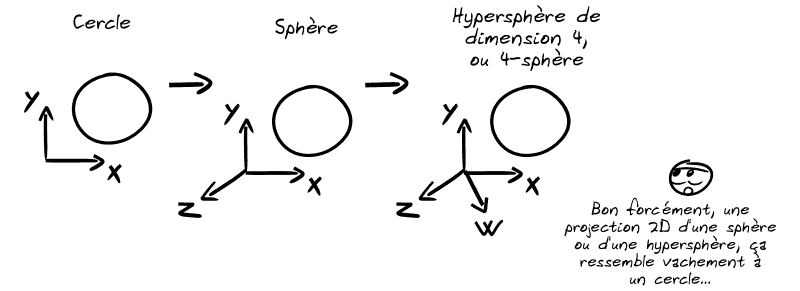
Bien sûr, les concepts comme la surface ou le volume se généralisent aussi…

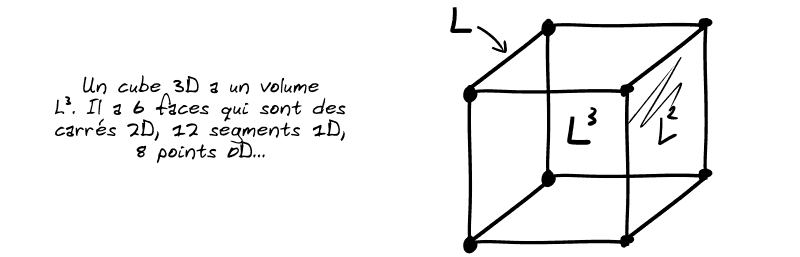
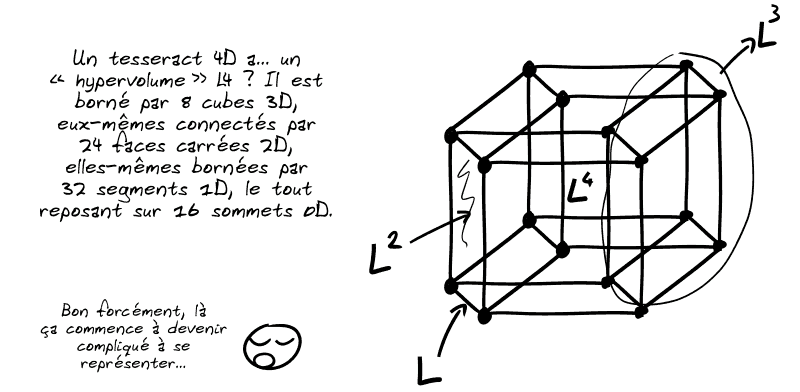
Et là, vous allez me poser la question qui tue…

➡ Eh bien par exemple, ça peut avoir des applications en statistiques…

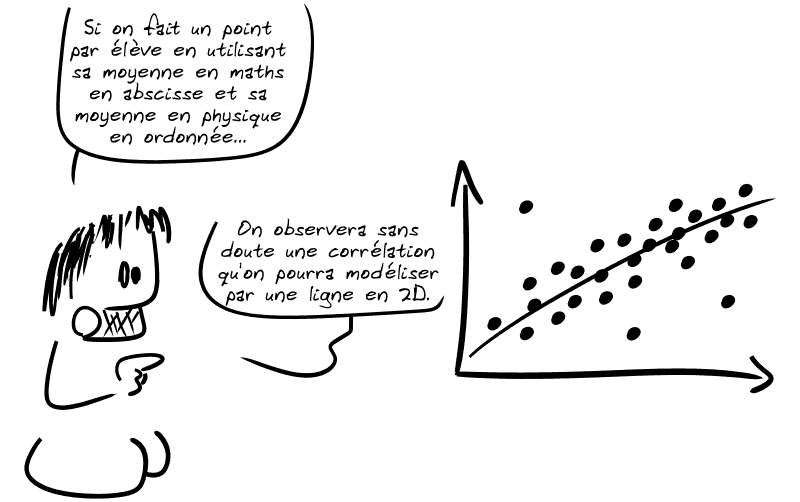
➡ Imaginons maintenant qu'on veuille faire le même genre de calcul mais en ajoutant les notes en SVT :

➡ Et si au lieu des SVT, on mettait une matière comme le français :

➡ Et si on avait trois matières complètement décorrélées :

💡 Eh bien on pourrait faire le même genre d'observations en ajoutant autant de matières qu'on veut, en 4D, 5D, 6D, etc. Ou n'importe quelles autres observations statistiques dont on voudrait étudier les corrélations croisées…

Avec des lignes, des surfaces, des volumes… et leurs équivalents en hautes dimensions.

Il n'y a aucune raison de limiter ces calculs à de la 3D juste parce qu'on peut la visualiser.

Bref, en conclusion : une 4^e dimension ajoutée à un espace 3D n'est pas nécessairement le temps, tout dépend en fait de ce qu'on veut modéliser.