L'effet râteau

Publié le 14 septembre 2022 par Gee dans Tu sais quoi ?

Aujourd'hui, on va causer un peu de statistiques, parce que c'est un domaine où il est trèèès facile de faire des erreurs de raisonnement…

L'effet râteau

Contrairement à ce que l'on pourrait imaginer de prime abord, l'effet râteau ne désigne pas la malchance en relations amoureuses.

Un mec regarde son téléphone : « J'ai un effet râteau sur Tinder : je me fais systématiquement ratisser vers la gauche… »

Pour comprendre l'effet râteau, regardez attentivement ces deux images :

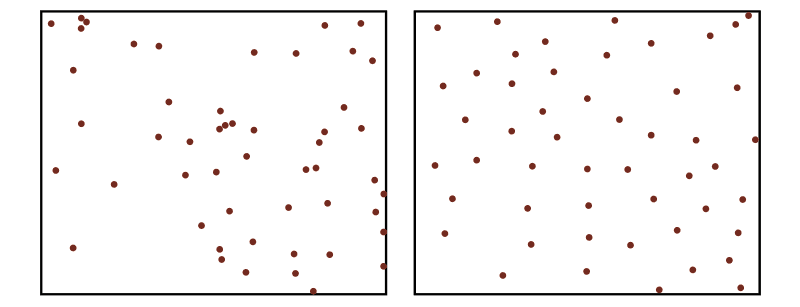
Deux distributions de points. À gauche, les points sont en vrac, certaines zones osont plus denses que d'autres ; à droite, les points ont l'air répartis au hasard, et la densité est assez uniforme.

Laquelle des deux images vous semble correspondre à une distribution où chaque point est choisi aléatoirement, indépendamment des autres ?

La Geekette : « T'en penses quoi, Jojo ? » Jojo : « Ben la deuxième, pardi ! Les points sont beaucoup mieux distribués sur la surface, alors qu'on sent qu'il y a des zones trop denses sur la première pour que ce soit bien aléatoire. »

Si vous vous êtes fait la même réflexion que Jojo, bravo : vous êtes victime de l'effet râteau !

Jojo, content : « Bravo… ça veut dire que j'ai gagné ? » La Geekette : « Ah non, tu t'es planté… mais bravo d'avoir illustré l'article ! » Le smiley : « Se planter avec l'effet râteau, ça va de soi… »

En effet, les points ont été tirés indépendamment sur la première image… alors que sur la deuxième, un critère a été ajouté pour rejeter un point s'il tombait trop près d'un autre. La position des points dépend donc des autres points.

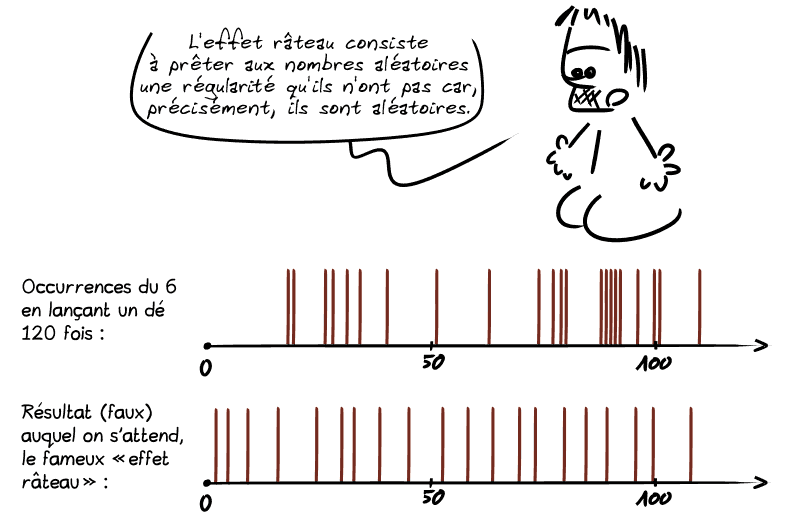
Face à une distribution régulière, on devrait au contraire, tel Paul McCartney, se poser les questions :

McCartney chante une parodie de « Eleanor Rigby » : « All the lonely events, where do they all come from? All the lonely events, where do they all belong?* »

« Tous ces événements isolés, d'où viennent-ils donc ? Tous ces événements isolés, à quelle distribution aléatoire appartiennent-ils donc ? » (traduction approximative)

Il semble que nous ayons tendance à surestimer l'aspect aléatoire de certains événements…

À la mer, Jojo fait remarquer : « Sur la plage, les serviettes sont plutôt uniformément distribuées, alors que les gens ne se concertent pas pour ça ! » La Geekette : « Eh oui Jojo, mais ce n'est pas aléatoire pour autant : on va avoir tendance à se placer loin des autres autant que possible… » Le smiley, avec un perruque de Beatle : « Jojo était un homme qui pensait être un solitaire… »

Tout en voyant des interdépendances entre plusieurs événements aléatoires successifs alors qu'il n'y en a pas…

Il y avait 3 % de chances de faire 5 fois « pile » de suite (0,5 puissance 5 est à peu près égale à 0,03125)… mais il y avait aussi 3 % de chances de faire, disons, « pile-face-pile-face-pile ».

Jojo : « D'accord… mais du coup, on avait 97 % de chance de ne PAS faire 5 fois de suite pile ! » La Geekette : « Oui… mais à partir du moment où ce tirage est tombé, bah il est tombé. Et tu gardes 50 % de chances de faire pile au prochain tirage. J'ai peu de chances de gagner au loto, mais si je gagne : je gagne, peu importe la probabilité de départ ! »

La foudre peut tomber deux fois au même endroit. Le fait qu'un événement ait une chance sur X de se produire ne signifie pas qu'il va nécessairement se produire une fois toutes les X occurrences…

Jojo : « Aujourd'hui, je vais gagner au loto ! » La Geekette : « Comment tu le sais ? » Jojo : « Bah on a une chance sur 19 millions de gagner, et c'est la 19 millionième fois que je joue… » La Geekette : « Oui, alors non, ça marche pas comme ça… » Le smiley : « Bon, après, si t'as les moyens de jouer 19 millions de fois au loto, est-ce que c'est bien utile d'y jouer ? »

Bref, soyons toujours prudents avec nos instincts vis-à-vis des statistiques… parce que c'est un coup à être victime d'effets comme l'effet râteau, et à faire des conneries.

Dans le tram, la Geekette demande au Geek : « T'as pas validé ton ticket ? » Le Geek, serein : « Boh non, je me suis déjà fait contrôler aujourd'hui… La foudre tombe pas deux fois au même endroit… » Note : BD sous licence CC BY SA (grisebouille.net), dessinée le 12 septembre 2022 par Gee.